机器学习中,我们的使用的数据基本都是高维的,所以我们很难直接从数据中观察分布和特征。因此出现了很多数据降维的手段帮助我们提取特征和可视化数据。这就是流行学习方法(Manifold Learning):假设数据是均匀采样于一个高维欧氏空间中的低维流形,流形学习就是从高维采样数据中恢复低维流形结构,即找到高维空间中的低维流形,并求出相应的嵌入映射,以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质,找到产生数据的内在规律。
有张图可以比较好的理解下降维的方法。
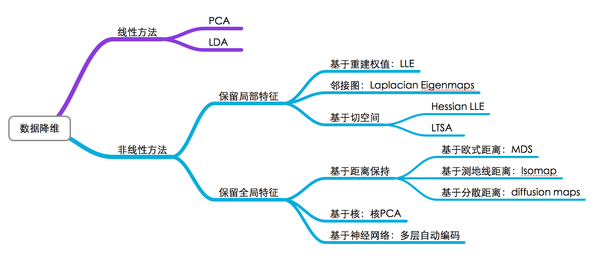
PCA曾经广泛用于提取特征,由于其是线性降维,所以不能解释特征之间的复杂多项式关系,而且也已经过于古老。而上图中没有提及的t-sne属于非线性方法,是由Hinton和lvdmaaten在2008年提出的。关于降维的数据作为feature是否更优还不能确定,但是其可视化效果非常好。由于t-sne运行速度非常慢,比pca高了一个数量级,因此在可视化数据的时候一般先用pca处理,然后再用tsne处理。
t-sne是由sne发展而来,SNE是通过仿射(affinitie)变换将数据点映射到概率分布上,主要包括两个步骤:
- SNE构建一个高维对象之间的概率分布,使得相似的对象有更高的概率被选择,而不相似的对象有较低的概率被选择。
- SNE在低维空间里在构建这些点的概率分布,使得这两个概率分布之间尽可能的相似
尽管SNE提供了很好的可视化方法,但是他很难优化,而且存在”crowding problem”(拥挤问题)。后续中,Hinton等人又提出了t-SNE的方法。与SNE不同,主要如下:
- 使用对称版的SNE,简化梯度公式
- 低维空间下,使用t分布替代高斯分布表达两点之间的相似度
具体的算法解释和推导可以关注这篇博文 http://www.datakit.cn/blog/2017/02/05/t_sne_full.html
优化mnist过程的动态图如下!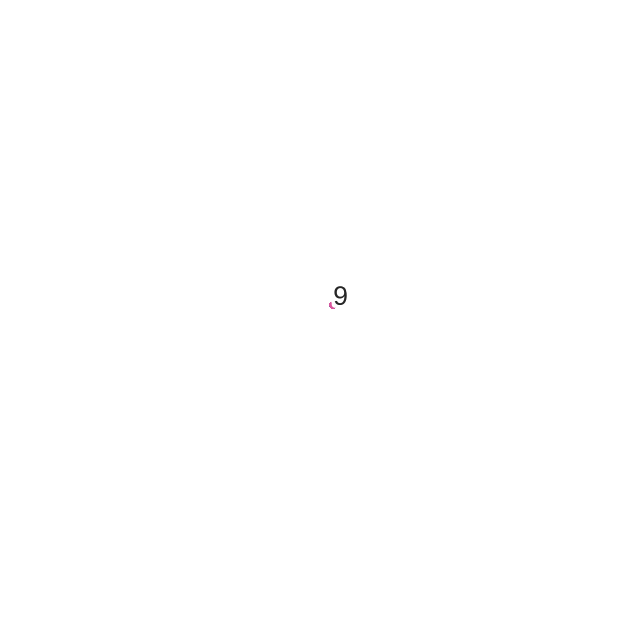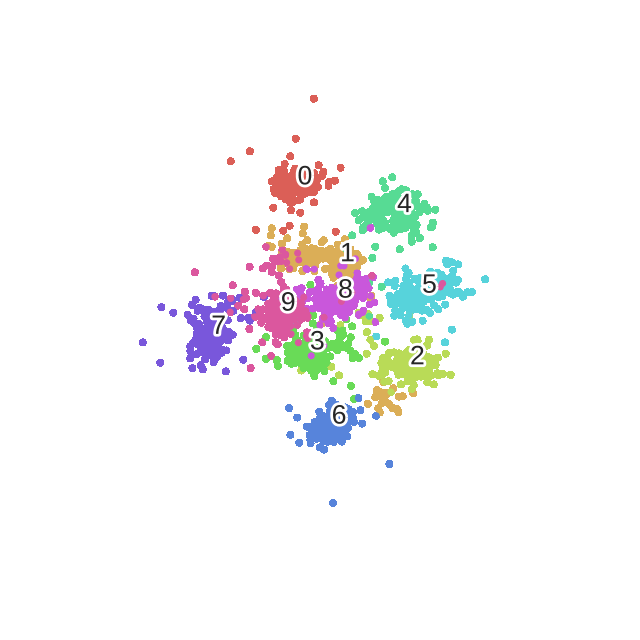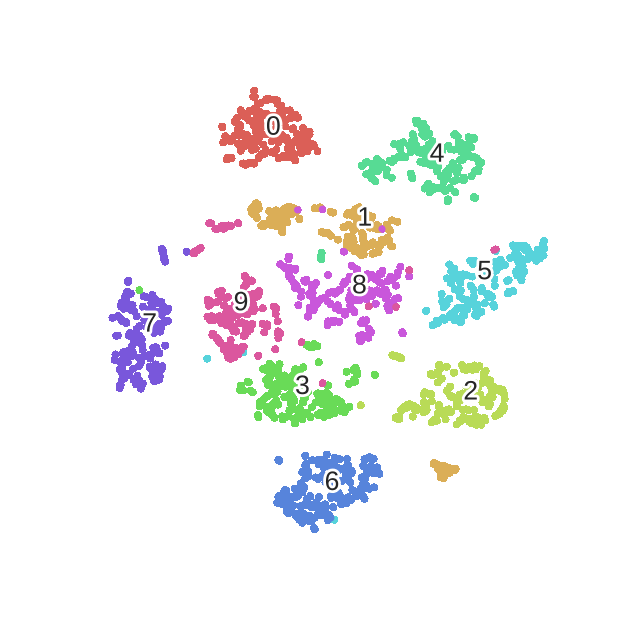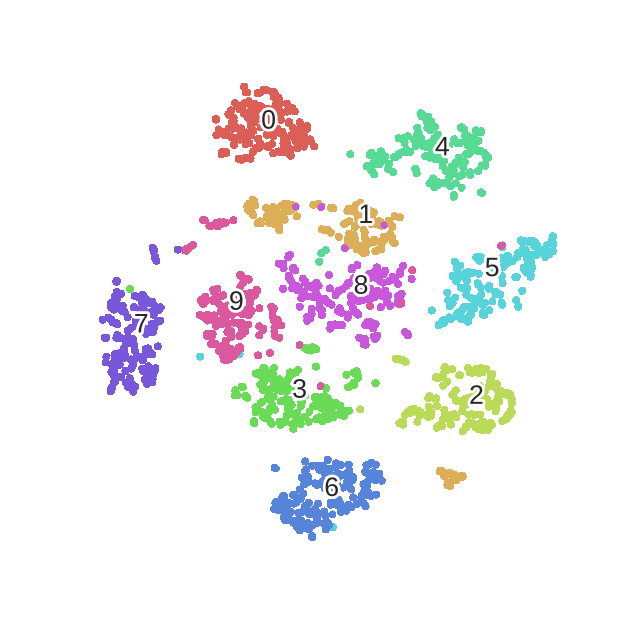
我们可以使用python得sklearn包来体验一下tsne,非常简单。
#import 相关的包和mnist数据集
import numpy as np
import matplotlib.pyplot as plt
from time import time
from sklearn import datasets, manifold
#定义函数将结果plot出来
def plot_embedding(X, title=None):
x_min, x_max = np.min(X, 0), np.max(X, 0)
X = (X - x_min) / (x_max - x_min)
plt.figure()
ax = plt.subplot(111)
for i in range(X.shape[0]):
plt.text(X[i, 0], X[i, 1], str(digits.target[i]),
color=plt.cm.Set1(y[i] / 10.),
fontdict={'weight': 'bold', 'size': 9})
plt.xticks([]), plt.yticks([])
if title is not None:
plt.title(title)
# 调用t-SNE
print("Computing t-SNE embedding")
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X)
plot_embedding(X_tsne,
"t-SNE embedding of the digits (time %.2fs)" %
(time() - t0))
plt.show()